Question

The curve with the equation y=8x^2 + 2/x has one turning point.

Find the coordinates of this turning point.

Answer 1

(1/2, 6).

Explanation:

Turning points in a graph may exist whenever the derivative equals 0. Hence, let’s differentiate and then solve our function.

We have:

`\displaystyle y=8x^2+(2)/(x)`

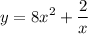
Take the derivative of both sides with respect to x:

`\displaystyle y^\prime=16x-(2)/(x^2)`

Simplify:

`\displaystyle y^\prime=(16x^3-2)/(x^2)`

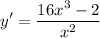
We will now set this equal to 0 and solve for x. Hence:

`\displaystyle \begin{aligned} 0&=(16x^3-2)/(x^2) \\ 0&=16x^3-2 \\ 2&=16x^3 \\ (1)/(8)&=x^3 \\ (1)/(2)&=x \end{aligned}`

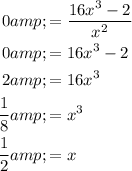
Hence, the graph turns at x=1/2. This is the x-coordinate.

Then it follows that the y-coordinate will be:

`\displaystyle{\begin{aligned} y&=8((1)/(2))^2+(2)/((1)/(2)) \\ y&=8(1/4)+2(2) \\ y&=2+4 \\ y&=6\end{aligned}`

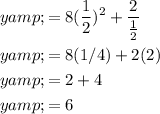
Hence, our coordinate Is (1/2, 6).