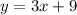Question

Determine the equation of the line that passes through the given points. (3,18) and (8,33)

Answer 1

Work out the gradient:
Change in Y/ Change in X
15/5 = 3
Plug this into linear equation of a line : Y=mx + c
Y=3x + c
To work out c plug in known point: 18 = (3)(3) + c
18 - 9 = c
C= 9
Therefore Y= 3x + 9

Answer 2

`y=3x+9`

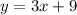
Explanation:

We want to determine the equation of the line that passes through the points (3, 18) and (8, 33).

First, let’s determine the slope. We can use the slope formula:

`m=(y_2-y_1)/(x_2-x_1)`

We will let (3, 18) be (x₁, y₁) and (8, 33) be (x₂, y₂). Then it follows that:

`\begin{aligned} m&=(33-18)/(8-3) \\ m&=(15)/(3) \\ m&=3\end{aligned}`

Hence, the slope is 3.

Now, we can use the point-slope form:

`y-y_1=m(x-x_1)`

We will substitute 3. for m. We can use either of the two points for (x₁, y₁) but let’s let (3, 18) be (x₁, y₁) for consistency. Thus:

`y-18=3(x-3)`

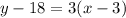
Then it follows that:

`\begin{aligned} y-18&=3x-9 \\ y&=3x+9 \end{aligned}`

Therefore, our equation is:

`y=3x+9`