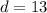Answer:
General Formulas and Concepts:
Pre-Algebra
- Order of Operations: BPEMDAS
- Equality Properties
Algebra I
Slope-Intercept Form: y = mx + b
The y-intercept is the y value when x = 0. Another way to reword that is when the graph crosses the y-axis.
The x-intercept is the x value when y = 0. Another way to reword that is when the graph crosses the x-axis.
Algebra II
- Distance Formula:
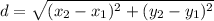
Explanation:
Step 1: Define
Equation 5x - 12y = 60
Step 2: Rewrite in slope-intercept form
- Isolate y term: -12y = 60 - 5x
- Isolate y: y = -5 + 5/12x
- Rewrite: y = 5/12x - 5
Step 3: Find x and y intercept
x-intercept
- Set y = 0: 0 = 5/12x - 5
- Isolate x term: 5 = 5/12x
- Isolate x: 12 = x
- Rewrite: x = 12
y-intercept
- Define: y = 5/12x - 5
- Break: y = -5
Step 4: Write coordinates
x-int (12, 0)
y-int (0, -5)
Step 5: Find distance d
- Substitute:
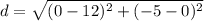
- Subtract:
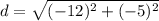
- Evaluate:
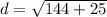
- Add:
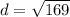
- Evaluate: