A. The ball's (vertical) velocity
 at time
at time
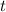 is
is
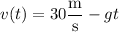
so that after 4 seconds, the ball's speed is
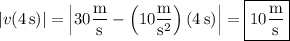
(The velocity is -10 m/s, so the ball is falling back down at this point.)
B. At maximum height, the ball has zero velocity, so it takes
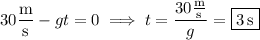
for the ball to reach this height.
C. The height of the ball
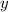 at time
at time
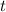 is
is
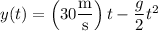
The maximum height is attained by the ball at 3 seconds after it's thrown, so
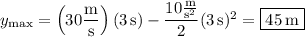
D. The time it takes for the ball to reach its maximum height is half the time it spends in the air. So the total airtime is
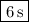 .
.
Put another way: When the ball returns to the height from which it was thrown, its final velocity has the same magnitude as its initial velocity but points in the opposite direction. This is to say, after the total time the ball is in the air, it's final velocity will be -30 m/s. Then the total airtime is
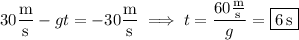
Put yet another way: Solve
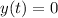 for
for
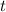 . I don't see a need to elaborate...
. I don't see a need to elaborate...