Question

What is the range of the function f(x)=-8x+13 when the domain is (-2,0,3)?

Answer 1

The complete set of domain (x) and range values (y) is given by:

x y

-2 39

0 13

3 11

Explanation:

Considering the function

`f(x)=-8x+13`

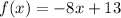
As we know that the range of a function consists of the entire set of all possible resulting values of the dependent variable commanly called y or f(x), once we have substituted the domain.

Now

• As the x values are -2, 0, and 3. So, the domain interval is (-2,0,3).

Putting x = -2 in f(x) to determine the range for the value x = -2

`f(x)=-8x+13`

`f(-2)=-8(-2)+13=16+13=39`

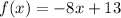
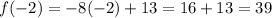
Putting x = 0 in f(x) determine the range for the value x = 0

`f(x)=-8x+13`

`f(0)=-8(0)+13=0+13=13`

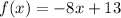
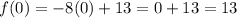
Putting x = 0 in f(x) determine the range for the value x = 3

`f(x)=-8x+13`

`f(3)=-8(3)+13=-24+13=11`

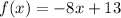
Therefore, the complete set of domain (x) and range values (y) is given by:

x y

-2 39

0 13

3 11