Answer:
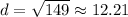
Explanation:
To find the distance between any two points, we can use the distance formula:
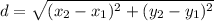
We have the two points (-1, 7) and (-8, -3).
Let (-1, 7) be (x₁, y₁) and let (-8, -3) be (x₂, y₂). Substitute:
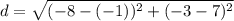
Evaluate:
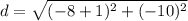
Evaluate:
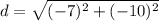
Square:
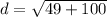
Add:
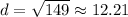
This cannot be simplified. Hence, the distance between (-1, 7) and (-8, -3) is √(149) or approximately 12.21 units.