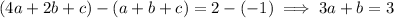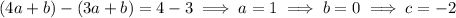Since we know it's quadratic, the n-th term will follow the pattern

for some unknown coefficients a, b, and c.
Given that
 ,
,
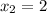 , and
, and
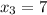 , we have the following conditions on these coefficients:
, we have the following conditions on these coefficients:

Solve this system to get a = 1, b = 0, and c = -2. Then
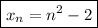
To solve the system, use elimination.