Answer:
C
Explanation:
We are given that:
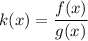
And we want to find k'(3).
So, let's find k'(x). Take the derivative of both sides. This will require the Quotient Rule. Hence:
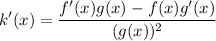
We want to find k’(3). Substitute:
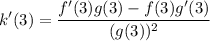
Using the table, make the appropriate substitutions:
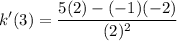
Evaluate:
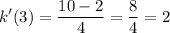
Therefore, our answer is C.