Question

There is strong believe that language skills of Political science students are greater than students who study Finance. Researcher selected some students from each faculty in order to assess this claim by using 95% confidence level. Language exam was taken from students for this purpose. It is assumed than unknown population variance of language skills for each faculty is the same. Exam results are given in the following table.

Observation Political Science Finance
1 7 5
2 4 3
3 8 7
4 8 8
5 7 9
6 7 5
7 6 5

a) Formulate Null and Alternative Hypothesis. (1 point)
b) Calculate p value of the test. (4 points)
c) What is your decision about Hypothesis? (2 points

Answer 1

a

The null hypothesis is
`H_o : \mu_1 = \mu_2`

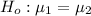
The alternative hypothesis
`H_a : \mu_1 > \mu_2`

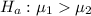
b

`p-value = 0.232`

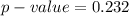
c

The decision rule is

Fail to reject the null hypothesis

Explanation:

From the question we are told that

The value given is

S/N

1 7 5

2 4 3

3 8 7

4 8 8

5 7 9

6 7 5

7 6 5

Generally the sample mean for the first sample is mathematically represented as

`\= x _1 = (\sum x_i )/(n)`

=>
`\= x _1 = (7 +4 + \cdots + 6)/(7)`

=>
`\= x _1 = 6.714`

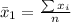
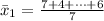
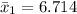
Generally the sample mean for the second sample is mathematically represented as

`\= x _2 = (\sum x_i )/(n)`

=>
`\= x _2 = (5 + 3+ \cdots + 5)/(7)`

=>
`\= x _2 = 6`

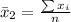
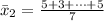
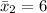
Generally the sample standard deviation for the first sample is mathematically represented as

`s_1 = \sqrt{(\sum (x_i - \= x_1)^2 )/(n-1 ) }`

=>
`s_1 = \sqrt{( (7 - 6.714 )^2 +(4 - 6.714 )^2 + \cdots + (6 - 6.714 )^2 )/(7-1 ) }`

=>
`s_1 = 1.905`

Generally the sample standard deviation for the second sample is mathematically represented as

`s_2 = \sqrt{(\sum (x_i - \= x_2)^2 )/(n-1 ) }`

=>
`s_2 = \sqrt{( (5 - 6.714 )^2 +(3 - 6.714 )^2 + \cdots + (5 - 6.714 )^2 )/(7-1 ) }`

=>
`s_1 = 4.33`

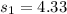
Generally the pooled standard deviation is

`s = \sqrt{((n_1 - 1 )s_1^2 + (n_2 - 1 )s_2^2)/(n_1 + n_2 -2 ) }`

=>
`s = \sqrt{((7 - 1 )1.905^2 + (7 - 1 )4.333^2)/(7 + 7 -2 ) }`

=>
`s = 1.766`

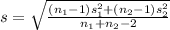
The null hypothesis is
`H_o : \mu_1 = \mu_2`

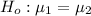
The alternative hypothesis
`H_a : \mu_1 > \mu_2`

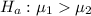
Generally the test statistics is mathematically represented as

`t = \frac{\= x _1 - \= x_2 }{s * \sqrt{(1)/(n_1) + (1)/(n_2)} }`

=>
`t = \frac{6.714 - 6 }{1.766 * \sqrt{(1)/(7) + (1)/(7)} }`

=>
`t = 0.757`

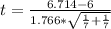
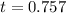
Generally the degree of freedom is mathematically represented as

`df = n_1 + n_2 - 2`

=>
`df = 7 + 7 - 2`

=>
`df = 12`

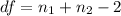
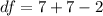
From the t distribution table the probability of
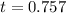`t = 0.757` at a degree of freedom of
`df = 12` is

`t_( 0.757 , 12) = 0.232`

Generally the p-value is

`p-value = t_( 0.757 , 12) = 0.232`

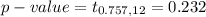
From the values obtained we see that
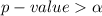`p-value > \alpha` hence

The decision rule is

Fail to reject the null hypothesis