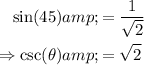Question

If 5cos^2θ + 6sin^2θ =11/2
, the value of cosecθ =--------

Answer 1

`\csc(\theta)=√(2)`

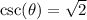
Explanation:

Please refer to the attachment below.

We have:

`5\cos^2(\theta)+6\sin^2(\theta)=11/2`

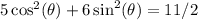
Remember that cosine is the ratio of the adjacent side to the hypotenuse. Therefore:

`\cos(\theta)=(b)/(c)`

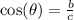
And sine is the ratio of the opposite side to the hypotenuse. Therefore:

`\sin(\theta)=(a)/(c)`

Substitute into our original equation:

`5((b)/(c))^2+6((a)/(c))^2=11/2`

Square:

`(5b^2)/(c^2)+(6a^2)/(c^2)=(11)/(2)`

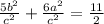
Multiply both sides by c squared:

`5b^2+6a^2=(11)/(2)c^2`

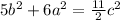
Let’s also multiply both sides by 2 to eliminate the fraction:

`10b^2+12a^2=11c^2`

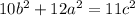
Remember that according to the Pythagorean Theorem:

`c^2=a^2+b^2`

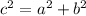
Hence, we can make another substitution:

`10b^2+12a^2=11(a^2+b^2)`

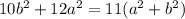
Distribute:

`10b^2+12a^2=11a^2+11b^2`

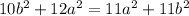
Subtract 10b² from both sides:

`12a^2=11a^2+b^2`

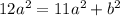
Subtract 11a² from both sides:

`a^2=b^2`

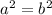
Take the square root of both sides:

`a=b`

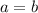
Hence, a is equivalent to b.

Then, we must have a 45-45-90 Triangle.

Therefore, our angle θ is 45°.

We can substitute this back into our original equation to make sure. Remember that cos(45)=sin(45)=√2/2:

`\begin{aligned} 5\cos^2(45)+6\sin^2(45)&=11/2 \\ 5((√(2))/(2)})^2+6((√(2))/(2))^2&=11/2 \\ 5(2/4)+6(2/4)&=11/2 \\ 5(1/2)+6(1/2)&=11/2 \\ 5/2+6/2&=11/2 \\ 11/2&=11/2 \;\checkmark \end{aligned} \\`

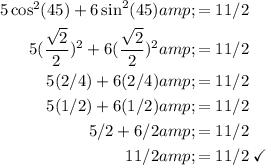
Hence:

`\begin{aligned} \sin(45)&=(1)/(√(2)) \\ \Rightarrow \csc(\theta)&=√(2) \end{aligned}`