Answer:
4 numbers
Explanation:
Given
Five Digit Flippy Numbers
Required
Determine the number of these digits divisible by 15
Represent the format of this digits as: ABABA
A number is divisible by 15 if and only if it ends with 5 or 0
i.e.
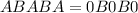
or
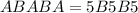
The first format
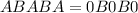 cannot be considered because the number starts with 0 which means that
cannot be considered because the number starts with 0 which means that
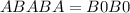 ---- This is 4 digits not 5
---- This is 4 digits not 5
Taking into consideration: 5B5B5
We know that 15 is a product of 5 and 3
i.e.
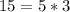
5B5B5 is divisible by 5 because it ends with 5. So, for a number of this format to be divisible by 15, it must be divisible by 3
Numbers in this category are: 50505, 53535, 56565 and 59595
Hence, there are 4 five-digit flippy numbers divisible by 5.