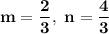Answer:
Step-by-step explanation:
Dimensional Analysis
It's given the relation between quantities A, B, and C as follows:
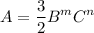
and the dimensions of each variable is:
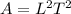
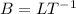
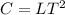
Substituting the dimensions into the relation (the coefficient is not important in dimension analysis):
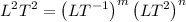
Operating:
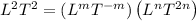

Equating the exponents:
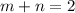
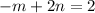
Adding both equations:

Solving:
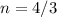
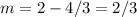
Answer: