Question

The x component of vector A is -25.0m and the y component id +40.0m (a) what is the magnitude of A?(b) What is the angle between the direction of A and the positive direction of x?

Answer 1

θ = 122°

Step-by-step explanation:

Components of a Vector

A vector in the plane can be defined by its rectangular components:

`\vec A =<x,y>`

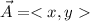
Or also can be given by its polar components:

`\vec A =<r,\theta>`

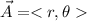
Where r is the magnitude of the vector and θ is the angle it forms with the positive direction of x.

The relation between them is:

`r=√(x^2+y^2)`

`\displaystyle \theta=\arctan(y)/(x)`

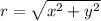
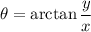
It's given the x-component of vector A is x=-25 m and the y-component is y=40 m

(a)

The magnitude of the vector is:

`r=√((-25)^2+40^2)`

`r=√(625+1600)`

`r=√(2225)`

`r\approx 47.2\ m`

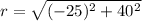
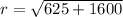
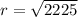
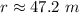
(b)

`\displaystyle \theta=\arctan(40)/(-25)`

`\displaystyle \theta=\arctan (-1.6)`

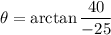
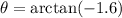
The calculator gives us the value

θ = -58°

But the real angle lies on the second quadrant since x is negative and y is positive, thus:

θ = -58° + 180° = 122°

θ = 122°