Answer:
One possible combination:
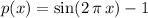 .
.
 .
.
 .
.
Explanation:
The requirement that
 for all
for all
 suggests that
suggests that
 should be a cyclic function with a period of
should be a cyclic function with a period of
 .
.
One such example is the sine function. Let
 denote a non-zero real number. Consider the expression
denote a non-zero real number. Consider the expression
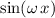 .
.
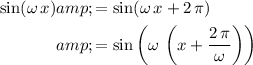 .
.
Note how replacing
 with
with
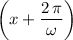 does not change the value of
does not change the value of
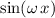 . Therefore, the period of
. Therefore, the period of
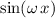 would be
would be
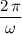 .
.
The question requires that replacing the
 with
with
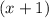 should not change the value of
should not change the value of
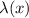 . In other words, the period of
. In other words, the period of
 should be
should be
 . If
. If
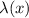 is indeed in the form
is indeed in the form
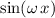 , the value of
, the value of
 should ensure that
should ensure that
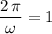 . Therefore,
. Therefore,
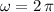 .
.
It would take a few more transformations to ensure that for all integers
 ,
,
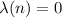 and
and
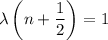 .
.
One possible approach is to make each
 a trough of this function, and each
a trough of this function, and each
 a crest of this function. The corresponding sine wave would have a range of only
a crest of this function. The corresponding sine wave would have a range of only
 . However, without any transformation,
. However, without any transformation,
 would have a range of two.
would have a range of two.
Therefore, it would be necessary to compress
 vertically by a factor of
vertically by a factor of
 , so that its range meets the needs.
, so that its range meets the needs.
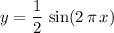 is the output of one such compression and has the correct period and range. However, its troughs would be at
is the output of one such compression and has the correct period and range. However, its troughs would be at
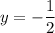 (rather than
(rather than
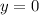 ) whereas its crests are at
) whereas its crests are at
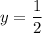 (rather than
(rather than
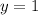 .) It would be necessary to shift this function upwards by
.) It would be necessary to shift this function upwards by
 unit for the troughs and crests to meet match the ones in the requirements.
unit for the troughs and crests to meet match the ones in the requirements.
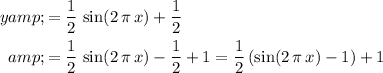 .
.