Question

the vertices of a triangle are located at (-3,-1), (2,3),(5,2). record the triangles perimeter to the nearest whole number

Answer 1

The perimeter of the triangle is approximately equal to 18

Explanation:

The coordinates of the vertices of the triangle are (-3, -1), (2, 3), and (5, 2)

The formula for the lengths, l, of the sides of the triangle, given their end points coordinates is presented as follows;

`l = \sqrt{\left (y_(2)-y_(1) \right )^(2)+\left (x_(2)-x_(1) \right )^(2)}`

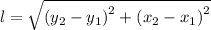
The lengths of the segments that make up the triangle are therefore;

Between the vertex points (-3, -1) and (2, 3), we have, √((-3 - 2)² + (-1 - 3)²) = √41

Between the vertex points (-3, -1) and (5, 2), we have, √((-3 - 5)² + (-1 - 2)²) = √73

Between the vertex points (2, 3) and (5, 2), we have, √((2 - 5)² + (3 - 2)²) = √10

Therefore;

The perimeter of the triangle = The sum of the lengths of the sides of the triangle = √41 + √73 + √10

The perimeter of the triangle = √41 + √73 + √10 ≈ 18.1094

∴ The perimeter of the triangle ≈ 18, after rounding to the nearest whole number.