Question

find the lump sum that must be deposited today to have a future value of $25,000 in 9 years if the funds carn 8%, compounded annually. Use the table of values below.

Answer 1

The lum sum that must be deposited today is $12,506.25 to have a future value of $25,000 in 9 years if the funds carn 8%, compounded annually.

Explanation:

We are given:

Future value (A)=$25,000

Rate r =8% (0.08%)

Time t = 9

Compounded Annually n =1

We need to find:

Principal Amount (P) = ?

The formula used will be:

`A=P(1+(r)/(n))^(nt)`

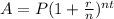
Putting values and finding Principal Amount (P)

`A=P(1+(r)/(n))^(nt)\\25000=P(1+(0.08)/(1))^(9*1) \\25000=P(1+0.08)^(9) \\25000=P(1.08)^(9) \\25000=P(1+0.08)^(9) \\25000=P(1.9990)\\P=(25000)/(1.9990)\\\mathbf{P=12506.25 }`

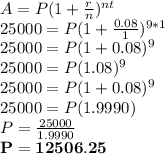
So, The lum sum that must be deposited today is $12,506.25 to have a future value of $25,000 in 9 years if the funds carn 8%, compounded annually.