Question

Given the sequence, 26, 13, 6.5, ..... find a) the 10th term and b) the sum of the first 18 terms

Answer 1

a) 10th term is 0.051

b) The sum of first 18 terms of given sequence is 51.48

Explanation:

We are given the sequence 26, 13, 6.5, ..... we need to find

a) 10th term

b) Sum of first 18 terms

Before solving we need to determine if the sequence is arithmetic or geometric

The sequence is arithmetic if common difference d is same.

The sequence is geometric if common ratio r is same.

Finding common difference d: 13-26 = -13, 6.5-13= -6.5

As common difference is not same so, the sequence is not arithmetic.

Finding common ratio r : 13/26 =0.5, 6.5/13= 0.5

As common ratio is same so, the sequence is geometric.

a) Finding common difference: 13-26 = -13, 6.5-13= -6.5

As common difference is not same so, the sequence is not arithmetic.

a) 10th term

The formula to find 10th term is:
`a_n=a_1r^(n-1)`

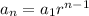
We have a₁=26 and r = 0.5 n=10

`a_n=a_1r^(n-1)\\a_(10)=26(0.5)^(10-1)\\a_(10)=26(0.5)^(9)\\a_(10)=0.051`

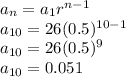
So, 10th term is 0.051

b) Sum of first 18 terms

The formula to find sum of geometric series is:
`S_n=(a(1-r^n))/(1-r)`

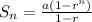
where a= 1st term, r = common ratio and n= number of terms

In the given sequence we have

a=26, r=0.5 and n=18

Finding sum of first 18 terms

`S_n=(a(1-r^n))/(1-r)\\S_(18)=(26(1-(0.5)^(18))/(1-0.5)\\S_(18)=(26(0.99))/(0.5)\\S_(18)=(25.74)/(0.5)\\S_(18)=51.48`

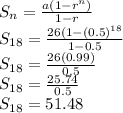
So, sum of first 18 terms of given sequence is 51.48