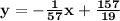Answer:
Equation of a line through (15, 8) that is perpendicular to the line y =57 x −1 is
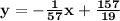
Explanation:
We need to write an equation of a line through (15, 8) that is perpendicular to the line y =57 x −1.
The equation will be in slope-intercept form:
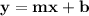
Where m is slope and b is y-intercept.
Finding Slope of new line
We are given equation
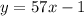 of line, which is perpendicular to the line whose equation we need to find.
of line, which is perpendicular to the line whose equation we need to find.
If the lines are perpendicular there slopes are inverse of each other i.e
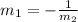
Slope of given line is m= 57 ( compare the given equation with standard slope-intercept form the value of m is 57
Slope of new line is m=
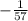
Finding y-intercept of new line
Now finding y-intercept (b) for new line. It can be found using point (15,8) and slope m =
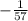
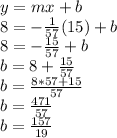
So, y-intercept b of new line is:
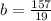
Equation of required line
Equation of line having slope m=
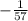 and y-intercept
and y-intercept
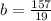 is:
is:
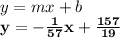
So, equation of a line through (15, 8) that is perpendicular to the line y =57 x −1 is