Question

Solve x+4/4 = x/x-2

Answer 1

After solving the equation
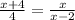`(x+4)/(4)=(x)/(x-2)` we get x=-2 and x= 4 i.e {-2,4}.

Option B is correct.

Explanation:

We need to solve
`(x+4)/(4)=(x)/(x-2)`

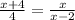
Solving:

`(x+4)/(4)=(x)/(x-2)`

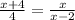
Cross multiply

`(x-2)(x+4)=x*4`

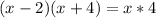
Multiplying:

`x(x+4)-2(x+4)=4x\\x^2+4x-2x-8=4x\\x^2+2x-8-4x=0\\x^2-2x-8=0`

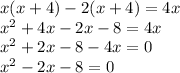
Now, we have got quadratic equation
`x^2-2x-8=0`

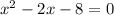
Solving this quadratic equation using quadratic formula

`x=(-b\pm√(b^2-4ac))/(2a)\\`

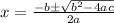
We have a=1, b=-2 and c=-8 Putting values

`x=(-b\pm√(b^2-4ac))/(2a)\\x=(-(-2)\pm√((-2)^2-4(1)(-8)))/(2(1))\\x=(2\pm√(4+32))/(2)\\x=(2\pm√(36))/(2)\\x=(2\pm6)/(2)\\x=(2+6)/(2) \ or \ x=(2-6)/(2)\\x=(8)/(2) \ or \ x=(-4)/(2)\\x=4 \ or \ x=-2`

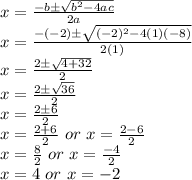
So,after solving the equation
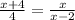`(x+4)/(4)=(x)/(x-2)` we get x=-2 and x= 4 i.e {-2,4}.

Option B is correct.