Question

Find the sum of the finite geometric series

6 - 4 + 8/3 - 16/9 + 32/17

Answer 1

The sum of geometric series 6 - 4 + 8/3 - 16/9 + 32/17 is 4.0416

Explanation:

We need to find the sum of geometric series 6 - 4 + 8/3 - 16/9 + 32/17

The formula used to find sum of geometric series is
`S_n=(a(1-r^n))/(1-r)`

where a is 1st term, n is number of terms and r is common ratio

so, in the given geometric series 6 - 4 + 8/3 - 16/9 + 32/17 we have

First Term a=6

Common ratio r= -0.6

Number of terms n= 5

Putting values in formula to find sum of given geometric series

`S_n=(a(1-r^n))/(1-r)\\S_n=(6(1-(-0.6)^5 ))/(1-(-0.6))\\S_n=(6(1-(-0.07776)))/(1+0.6)\\S_n=(6(1+0.07776))/(1.6)\\S_n=(6.46656)/(1.6)\\S_n=4.0416`

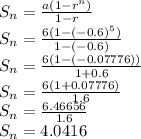
So, the sum of geometric series 6 - 4 + 8/3 - 16/9 + 32/17 is 4.0416