We are integrating f(x) = 9cos(9x) + 3x²:
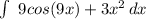
a) Apply the sum rule
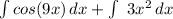
b) Calculate each antiderivative
First integral
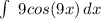
1. Take out the constant
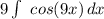
2. Apply u-substitution, where u is 9x
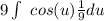
3. Take out the constant (again)
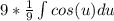
4. Take the common integral of cos, which is sin
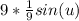
5. Substitute the original function back in for u and simplify
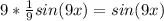
6. Always remember to add an arbitrary constant, C, at the end
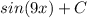
Second integral
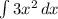
1. Take out the constant
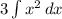
2. Apply the power rule,
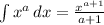 , where a is your exponent
, where a is your exponent
⇒
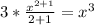
3. Add the arbitrary constant
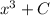
c) Add the integrals
sin(9x) + C + x³ + C = sin(9x) + x³ + C
Notice the two arbitrary constants. Since we do not know what either constant is, we can combine them into one arbitrary constant.
Answer:
F(x) = sin(9x) + x³ + C