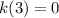Question

A function k whose domain is the set of positive integers is defined as k(1) = 4 and k(n) =

k(n - 1) - 2
Function k was evaluated for several numbers. Which of the following are true?
Select each correct answer.

Answer 1

k(2)=

• k(1)-2
• 4-2
• 2

Option C is true

k(3)

• k(2)-2
• 2-2
• 0

D is true

k(4)

• k(3)-2=0-2=-2

k(5)

• -2-2
• -4

k(6)

• -4-2
• -6

E is not true

k(1)

• k(0)-2

So

• k(0)-2=4
• k(0)=6

B is false

Similarly

• k(-1)-2=k(0)=6
• k(-1)=8

-1 is not in domain even though

A is false

Only C and D are true

Answer 2

`k(2) = 2`

`k(3) = 0`

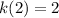
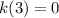
Explanation:

Given:

`\begin{cases}k(1)=4\\k(n)=k(n-1)-2\end{cases}`

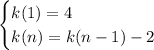
The function
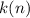`k(n)` tells us that each term is 2 less than the preceding term.

Therefore:

`\implies k(1)=4`

`\implies k(2)=k(1)-2=4-2=2`

`\implies k(3)=k(2)-2=2-2=0`

`\implies k(4)=k(3)-2=0-2=-2`

`\implies k(5)=k(4)-2=-2-2=-4`

`\implies k(6)=k(5)-2=-4-2=-6`

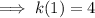
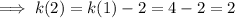
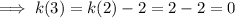
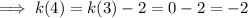
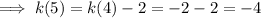
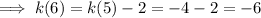
Rearranging the formula to make the preceding term the subject:

`\begin{aligned} k(n) & = k(n-1) - 2\\\implies k(n)+2 & = k(n-1)\\k(n-1) & =k(n)+2\end{aligned}`

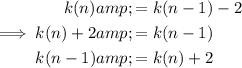
Therefore:

`\implies k(1)=4`

`\implies k(0)=k(1)+2=4+2=6`

`\implies k(-1)=k(0)+2=6+2=8`

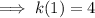
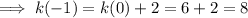
Conclusion

Therefore, the correct answers from the answer options are:

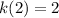`k(2) = 2` and
`k(3) = 0`