A second-degree polynomial takes the form
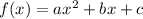
for some constants a, b, and c. Such a function is continuous and differentiable everywhere in its domain.
Differentiating f(x) with respect to x gives
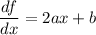
We're told that
• f(x) is increasing on [0, 8]
• f(x) is decreasing on ]-10, 0]
and since df/dx is continuous, this tells us that df/dx = 0 when x = 0. It follows that b = 0, and we can write
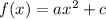
We're also given that the curve passes through the point (-8, 4), which gives rise to the constraint
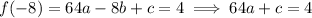
Since f(x) is decreasing on ]-10, 0], we have df/dx < 0 when x = -8, so
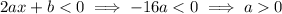
This means f(x) is minimized when x = 0, with min{f(x)} = c, so the co-domain of f(x) is the set {f(x) ∈ ℝ : f(x) ≥ c}.
Without another condition, that's all we can say about the co-domain. There are infinitely many choices for the constants a and c that satisfy the given conditions. For example,
a = 1, c = -60 ⇒ f(x) = x² - 60 ⇒ f(-8) = 4
⇒ co-domain = {f(x) ∈ ℝ : f(x) ≥ -60}
a = 2, c = -124 ⇒ f(x) = 2x² - 124 ⇒ f(-8) = 4
⇒ co-domain = {f(x) ∈ ℝ : f(x) ≥ -124}
etc.