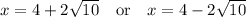Answer: Choice C)

This is the same as saying
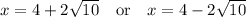
=============================================================
Step-by-step explanation:
First get everything to one side
x^2 + 13 = 8x + 37
x^2 + 13 - 8x - 37 = 0
x^2 - 8x - 24 = 0
Here we have a quadratic in the form ax^2+bx+c = 0
Note how a = 1, b = -8, c = -24
Those values are plugged into the quadratic formula below

This shows the answer is choice C.
The plus minus breaks down that equation these two solutions