Question

←

How many solutions does this linear system have
y =
x+2
6x - 4y = -10

Answer 1

This linear system has one solution.

Explanation:

First equation: y = x + 2

Second equation: 6x - 4y = -10

Let's change the second equation in slope-intercept form y = mx + b.

Slope-intercept form

y = mx + b

m ... slope

b ... y-intercept

`6x - 4y = -10`

`6x + 10 = 4y`

`(6)/(4)x + (10)/(4) = y`

`(3)/(2)x + (5)/(2) = y`

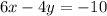
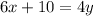
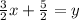
If two lines have the same slope but different y-intercept, they are parallel - system has no solutions.

If two lines have the same slope and the same y-intercept, they are the same line and are intersecting in infinite many points - system has infinite many solutions.

If two lines have different slopes then they intersect in one point - system has one solution.

We see that lines have different slopes. First line has slope 1 and the other line has slope
`(3)/(2)`. So the system has one solution.

You can also check this by solving the system.

Substitute y in second equation with y from first.

6x - 4y = -10

6x - 4(x + 2) = -10

Solve for x.

6x - 4x - 8 = -10

2x = -2

x = -1

y = x + 2

y = -1 + 2

y = 1

The lines intersect in point (-1, 1). <-- one solution