Answer:

Step-by-step explanation:
Newton's Law of Universal Gravitation:
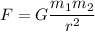
- F = force of gravity (N)
- G = gravitational constant
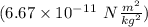
 = mass of Object 1 (kg)
= mass of Object 1 (kg)
 = mass of Object 2 (kg)
= mass of Object 2 (kg)- r = distance between the center of mass (m)
Let's convert our given information to scientific notation:
Now using the gravitational force and the distance between centers of mass that are given, we can plug these into Newton's law:
Remove the units for better readability.
Divide both sides of the equation by the gravitational constant G.
Distribute the power of 2 inside the parentheses.
If we evaluate the left side of the equation, we get:
Multiply both sides of the equation by r.
In order to find the mass of one asteroid, we can use the fact that both asteroids have the same mass, therefore, we can rewrite
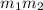 as
as
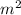 .
.
Square root both sides of the equation.
Since m is in units of kg, we can state that the mass of each asteroid is 2.79 * 10⁵ kg.