Question

Two complex numbers have a product of 30 and positive integers as real parts. Write all possible combinations of such numbers.

Answer 1

`[(1+i√(29)), (1-i√(29))]`,
`[(1+i√(26)), (1-i√(26))]`,
`[(1+i√(21)), (1-i√(21))]`,

`[(1+i√(14)), (1-i√(14))]`, and
`[(1+i√(5)), (1-i√(5))]`.

Explanation:

Given that two complex numbers have a product of 30 and the real part of the complex numbers are positive integers.

Let one complex number is
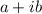`a+ib` where
`a` is a positive integer and
`b` is a real number.

As the product of two complex numbers is a purely real number, so the other complex number must be the conjugate of the first complex number.

So, another complex number
`= a-ib`

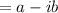
As a product of both the numbers = 30

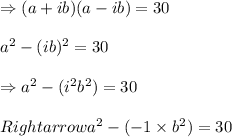`\Rightarrow (a+ib)(a-ib)=30 \\\\\Rightarroe a^2 - (ib)^2=30 \\\\\Rightarrow a^2 - (i^2b^2)=30 \\\\Rightarrow a^2 - (-1* b^2)= 30` [as i^2=-1]

`\Rightarrow a^2+b^2= 30 \\\\\Rightarrow b^2 = 30-a^2 \\\\`

`\Rightarrow b=\pm \sqrt {30-a^2} \cdots(i)`

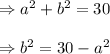
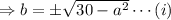
Now, as a is a positive integer, so by taking possible values of a, we can determine the values of b from the equation (i).

For
`a=1`

`b=\pm \sqrt {30-1^2}=\pm \sqrt {29}`

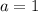
The positive sign is for the one number and the negative sign is for the conjugate number (another number).

So, the 1st combination is
`[(1+i√(29)), (1-i√(29))]`

Similarly,

For
`a=2`

`b=\pm \sqrt {30-2^2}=\pm \sqrt {26}`

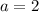
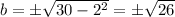
So, the 2nd combination is
`[(1+i√(26)), (1-i√(26))]`

For
`a=3`

`b=\pm \sqrt {30-3^2}=\pm \sqrt {21}`

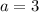
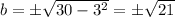
So, the 3rd combination is
`[(1+i√(21)), (1-i√(21))]`

For
`a=4`

`b=\pm \sqrt {30-4^2}=\pm \sqrt {14}`

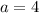
So, the 4th combination is
`[(1+i√(14)), (1-i√(14))]`

For
`a=5`

`b=\pm \sqrt {30-5^2}=\pm \sqrt {5}`

So, the 5th combination is
`[(1+i√(5)), (1-i√(5))]`

The higher integral value of
`a` is not possible for any real
`b`.

Hence, the possible combinations of required numbers are

`[(1+i√(29)), (1-i√(29))]`,
`[(1+i√(26)), (1-i√(26))]`,
`[(1+i√(21)), (1-i√(21))]`,

`[(1+i√(14)), (1-i√(14))]`, and
`[(1+i√(5)), (1-i√(5))]`.