Final answer:
The function f(x) = -
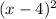 + 5 satisfies the range y ≤ 5 because its maximum value is 5 and it opens downwards.
+ 5 satisfies the range y ≤ 5 because its maximum value is 5 and it opens downwards.
Step-by-step explanation:
The function with a range of y ≤ 5 is the one where the highest value that y can take is 5. The function f(x) = −
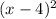 + 5 has a vertex at the point (4, 5) and opens downwards, as indicated by the negative sign in front of the quadratic term. This means that as x moves away from 4 in either direction, the value of the function decreases, which confirms the function's range will not exceed y = 5.
+ 5 has a vertex at the point (4, 5) and opens downwards, as indicated by the negative sign in front of the quadratic term. This means that as x moves away from 4 in either direction, the value of the function decreases, which confirms the function's range will not exceed y = 5.
On the other hand, the function f(x) =
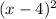 + 5 has a minimum value at x = 4, after which its values keep increasing as x moves away from 4. The function f(x) =
+ 5 has a minimum value at x = 4, after which its values keep increasing as x moves away from 4. The function f(x) =
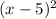 + 4 has a minimum point at (5, 4), and f(x) = −
+ 4 has a minimum point at (5, 4), and f(x) = −
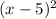 + 4 has a maximum point at (5, 4). Both of these functions do not have the range specified because they either only achieve y = 4 or continue increasing above y = 5.
+ 4 has a maximum point at (5, 4). Both of these functions do not have the range specified because they either only achieve y = 4 or continue increasing above y = 5.