Question

Calc BC problems. Need work

Answer 1

f'(0) = -2

f'(-2) = dne

`\lim_(h \to 0^+) (f(2+h)-f(2))/(h) = \text{does not exist}`

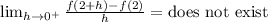
Explanation:

The question specifically asks us to use the graph of the function to evaluate the following problems.

In order to find the derivative of a function at a specific point on the graph:

1. Choose the point on the graph where you want to find the derivative.
2. Figure out the tangent line to this point; this will be the line tangent to the curve of the graph at this point.
3. The slope of this tangent line is the derivative at this certain point on the graph.

In order to find f'(0), find x = 0 on the graph. This is at the origin. Now, draw a line tangent to the curve of the graph at x = 0.

This tangent line will follow the same direction as the original function. So, we want to find the slope tangent line now - we can do so by finding the slope of the graph between the interval [-2, 2].

Slope of tangent line for f'(0):

• Slope formula:
  `(y_2-y_1)/(x_2-x_1)`
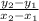
• Use coordinate points (-1, 2) and (1, -2)
• Slope of tangent line:
  `(-2-2)/(1-(-1)) = (-4)/(2) =-2`

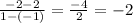
The slope of the tangent line for f'(0) is -2, therefore, this is the derivative at this point on the graph.

This is solving the problem graphically/algebraically, but you could also look at the graph and determine the rise/run in your head. Your choice.

Now, for f'(-2), we cannot use the same process as before since the graph shows that there is a sharp point at x = -2. This is called a "corner" and means that while the function is continuous, it is not differentiable.

Therefore, we can write that at f'(-2), the derivative does not exist (dne).

The same process occurs for f'(2), since there is a sharp point here. The derivative, based on the graph, does not exist.