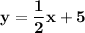Answer:
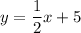
Explanation:
Equation of the line
The slope-intercept form of a line is given by:

Being:
m = the slope of the line
b = the y-intercept
We can also use the point-slope form of the line:

Being:
(h,k) = A point that belongs to the line
Two lines of slopes m1 and m2 are perpendicular if:
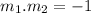
We are given the line:
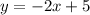
Whose slope is m1=-2
Thus, the perpendicular line has a slope of:
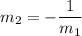
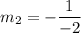
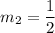
The required line contains the point (-8,1), thus the equation is:
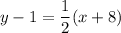
Removing the parentheses:

Adding 1:

Operating: