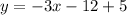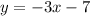Answer:
14.
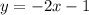
15.
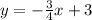
16.
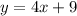
17.
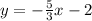
18.
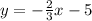
19.
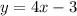
20.
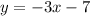
Explanation:
Solving (14):
Given
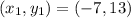
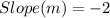
Equation in
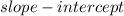 form is:
form is:
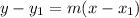
Substitute values for y1, m and x1
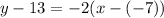
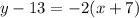
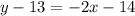
Collect Like Terms
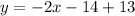
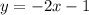
Solving (15):
Given
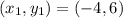
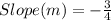
Equation in
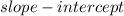 form is:
form is:
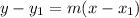
Substitute values for y1, m and x1
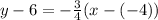
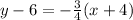
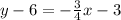
Collect Like Terms
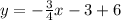
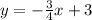
Solving (16):
Given
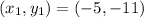
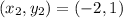
First, we need to calculate the
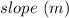
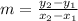
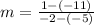
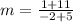
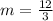
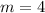
Equation in
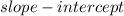 form is:
form is:
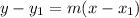
Substitute values for y1, m and x1
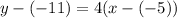
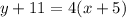
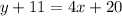
Collect Like Terms
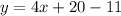
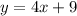
Solving (17):
Given
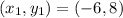
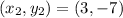
First, we need to calculate the
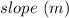
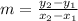
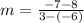
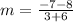
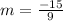
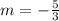
Equation in
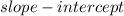 form is:
form is:
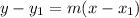
Substitute values for y1, m and x1
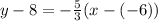
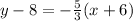
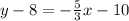
Collect Like Terms
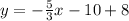
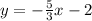
18.
Given
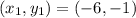
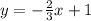
Since the given point is parallel to the line equation, then the slope of the point is calculated as:
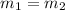
Where
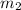 represents the slope
represents the slope
Going by the format of an equation,
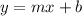 ; by comparison
; by comparison
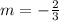
and
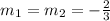
Equation in
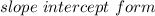 is:
is:
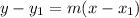
Substitute values for y1, m and x1
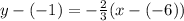
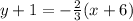
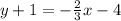
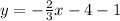
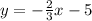
19.
Given
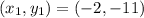
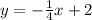
Since the given point is parallel to the line equation, then the slope of the point is calculated as:
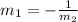
Where
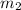 represents the slope
represents the slope
Going by the format of an equation,
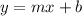 ; by comparison
; by comparison
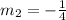
and
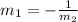
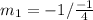
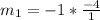
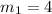
Equation in
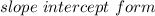 is:
is:
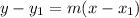
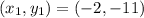
Substitute values for y1, m and x1
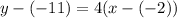
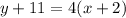
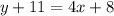
Collect Like Terms
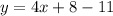
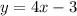
20.
Given
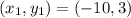
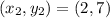
First, we need to calculate the slope of the given points
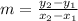
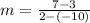
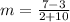
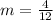
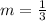
Next, we determine the slope of the perpendicular bisector using:
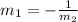
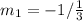
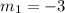
Next, is to determine the coordinates of the bisector.
To bisect means to divide into equal parts.
So the coordinates of the bisector is the midpoint of the given points;
![Midpoint = [(1)/(2)(x_1+x_2),(1)/(2)(y_1+y_2)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/kvxn4s8rsdmefd298dqc35neypoow0mm3c.png)
![Midpoint = [(1)/(2)(-10+2),(1)/(2)(3+7)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/xkix3rxh7p52669oq157pmqszia23y5jrt.png)
![Midpoint = [(1)/(2)(-8),(1)/(2)(10)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/bqimx6xq6zewqk15p7u3ymqdb3paa3vsjc.png)
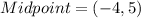
So, the coordinates of the midpoint is:
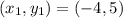
Equation in
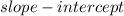 form is:
form is:
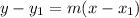
Substitute values for y1, m and x1:
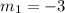 &
&
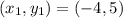
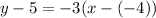
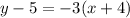
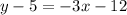
Collect Like Terms