Question

If the sine ratio is given, then how can sin 0/2 be determined?

Answer 1

Explanation:

If you know, the sine. You must find the cos ratio, using the Pythagorean trig theorem.

Next, you use the half angle identity for sin

`\sin( ( \alpha )/(2) ) = \sqrt{ (1 - \cos(a) )/(2) }`

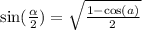
Example.

`\sin( \alpha ) = ( √(3) )/(2)`

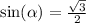
We must find

`\sin( ( \alpha )/(2) )`

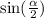
First, use the Pythagorean identity

`\sin {}^(2) ( \alpha ) + \cos {}^(2) ( \alpha ) = 1`

`( ( √(3) )/(2) ) {}^(2) + \cos {}^(2) (a) = 1`

`(3)/(4) + \cos {}^(2) (a) = 1`

`\cos {}^(2) (a) = (1)/(4)`

`\cos( \alpha ) = (1)/(2)`

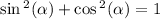
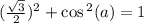
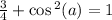
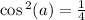
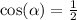
Now use the half angle identiy

`\sin( ( \alpha )/(2) ) = \sqrt{ (1 - \cos( \alpha ) )/(2) }`

`= \frac{ \sqrt{1 - (1)/(2) } }{ √(2) }`

`= \frac{ \sqrt{ (1)/(2) } }{ √(2) }`

`= \frac{ \sqrt{ (1)/(2) } }{ √(2) } * ( √(2) )/( √(2) ) = ( √(1) )/( √(4) ) = (1)/(2)`

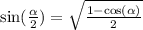
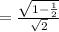
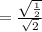
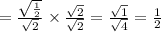
So the answer for our example is 1/2