Question

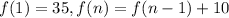
Find the recursive rule, explicit rule, and f(20)

Answer 1

Recursive:

`f(1)=35, f(n)=f(n-1)+10`

Explicit:

`f(n)=35+10(n-1)`

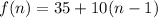
And the 20th term is 225.

Explanation:

We have the sequence:

35, 45, 55, 65.

Notice that each subsequent term is 10 more than the previous term.

Therefore, our common difference is (+)10.

Recursive Rule:

The standard format for the recursive rule is:

`f(n)=a, f(n)=f(n-1)+d`

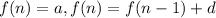
Where a is the initial term and d is the common difference.

From our sequence, we know that a the initial term is 35.

And as determined, our common difference d is 10.

Substitute. Hence, our recursive rule is:

`f(1)=35, f(n)=f(n-1)+10`

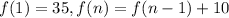
Explicit Rule:

The standard format for the explicit rule is:

`f(n)=a+d(n-1)`

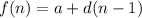
Where a is the initial term and d is the common difference. So, let’s substitute 35 for a and 10 for d. Hence, our explicit formula is:

`f(n)=35+10(n-1)`

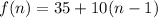
Now, let’s find the 20th term. We will utilize the explicit rule since the recursive rule can get tedious. Substitute 20 for n because we would like to 20th term. Thus:

`f(20)=35+10(20-1)`

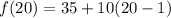
Evaluate:

`\begin{aligned} f(20)&=35+10(19) \\ f(20)&=35+190 \\ f(20)&=225 \end{aligned}`

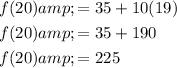
Hence, the 20th term is 225.