Question

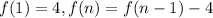
Find the recursive rule, explicit rule, and f(20)

Answer 1

Recursive:

`f(1)=4, f(n)=f(n-1)-4`

Explicit:

`f(n)=4-4(n-1)`

And the 20th term f(20) is -72.

Explanation:

We have the sequence:

4, 0, -4, -8...

Let’s find the recursive and explicit rule for the sequence.

Recursive Rule:

Let’s determine the factor by which the sequence is decreasing by. We see that each subsequent term is 4 less than the previous term. In other words, our common difference is -4.

So, this is a arithmetic sequence.

The standard format for an recursive rule for an arithmetic sequence is:

`f(1)=a , f(n)=f(n-1)+(d)`

Where a is the initial term and d is our common difference.

From our sequence, we know that our initial term a is 4.

We also determined that our common difference is -4.

Substitute. Hence, our recursive rule is:

`f(1)=4, f(n)=f(n-1)-4`

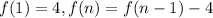
Explicit Rule:

The standard format for an explicit rule for an arithmetic sequence is:

`f(n)=a+d(n-1)`

Where a is the initial term and d is the common difference. So, again, let’s substitute 4 for a and -4 for d. Hence, our explicit formula is:

`f(n)=4-4(n-1)`

To find f(20), we can use the explicit formula. It is possible to use the recursive formula, but it gets tedious. Therefore, we will substitute 20 for n for our explicit formula:

`f(20)=4-4(20-1)`

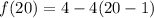
Evaluate:

`\begin{aligned} f(20)&=4-4(19) \\ f(20)&=4-76 \\ f(20)&=-72 \end{aligned}`

Hence, our 20th term is -72.