Question

What is the 7th term of the geometric sequence below? 7,-14,28,-56​

Answer 1

A

Explanation:

Answer 2

The 7th term of given sequence is: 448

Explanation:

Given sequence is:

7,-14,28,-56​

Here

a1 = 7

a2 = -14

a3 = 28

First of all we have to find the common ratio. The common ration is the ratio between two consecutive terms of a geometric sequence and is same for all consecutive terms of a geometric sequence.

So,

`r = (a_2)/(a_1) = (-14)/(7) = -2\\r = (a_3)/(a_2) = (28)/(-14) = -2\\`

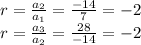
The common ratio is -2.

The general formula for geometric sequence is given as:

`a_n = a_1r^((n-1))`

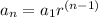
Putting values

`a_n = 7.(-2)^(n-1)`

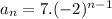
For 7th term, putting n=7

`a_7 = 7*(-2)^(7-1)\\= 7 * (-2)^6\\= 7 *64\\= 448`

Hence,

The 7th term of given sequence is: 448