Question

Given that f(x)=4x3-12x2+10 and g(x)=x3 – 2x2 + 5x

The value of f(x)- g(x)= ax'+bx?+ cx+d. What are the values of the coefficients a,b,c,d?

Answer 1

The values of a,b,c and d are as follows:

a = 3, b = -12, c = -5, d = 10

Explanation:

Given functions are:

`f(x) = 4x^3-12x^2+10\\g(x) = x^3-2x^2+5x`

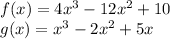
We have to find the value of f(x) - g(x). This means we have to subtract function g(x) from function f(x)

So,

`f(x) - g(x) = (4x^3-12x^2+10)-(x^3-2x^2+5x)\\= 4x^3-12x^2+10-x^3+2x^2-5x`

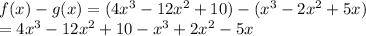
Combining alike terms

`= 4x^3-x^3-12x^2+2x^2-5x+10\\= 3x^3-10x^2-5x+10`

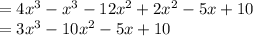
Now it was given that:

f(x)- g(x)= ax^3+bx^2+ cx+d

By comparing both we get

a = 3, b = -12, c = -5, d = 10

Hence,

The values of a,b,c and d are as follows:

a = 3, b = -12, c = -5, d = 10