Question

Find at least one solution to the following equation:

sin(x
2 − 1)
1 − sin(x
2 − 1) = sin(x) + sin2
(x) + sin3
(x) + sin4
(x) + · · ·

Answer 1

For |x| < 1, we have

`1+x+x^2+\cdots=\displaystyle\sum_(n\ge0)x^n=\frac1{1-x}`

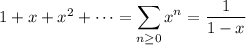
We have |sin(x)| ≤ 1, with equality when x = ± π/2. For either of these, the right side of the equation does not converge, since it's either an infinite sum of 1s or an infinite alternating sum of 1 and -1.

So for |sin(x)| < 1, we have

`\sin(x)+\sin^2(x)+\sin^3(x)+\cdots=\frac1{1-\sin(x)}-1=(\sin(x))/(1-\sin(x))`

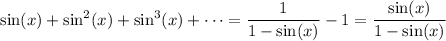
so the equation is equivalent to

`(\sin(x^2-1))/(1-\sin(x^2-1))=(\sin(x))/(1-\sin(x))`

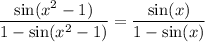
One obvious set of solutions occurs when x = x² - 1 :

x² - x - 1 = 0 → x = (1 ± √(5))/2

i.e. the golden ratio φ ≈ 1.618 and 1 - φ ≈ 0.618.