Answer:
The measure of ∠ZPX is 63°
Explanation:
The given parameters are;
The incenter of the triangle = P
m∠KXP = 31°, m∠PYJ = 27°,
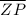 = 20 feet
= 20 feet
Given that the segment
 from the vertex, X, passes through the incenter of the triangle, we have;
from the vertex, X, passes through the incenter of the triangle, we have;
The segment
 bisects ∠KXL to form ∠KXP and ∠LXP
bisects ∠KXL to form ∠KXP and ∠LXP
Therefore, ∠KXP = ∠LXP = 31°
∠KXL = ∠KXP + ∠LXP = 31° + 31° = 62°
∠KXL = 62°
Similarly;
The segment
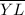 bisects ∠KYJ to form ∠PYJ and ∠PYK
bisects ∠KYJ to form ∠PYJ and ∠PYK
Therefore, ∠PYJ = ∠PYK = 27°
∠KYJ = ∠PYJ + ∠PYK = 27° + 27° = 54°
∠KYJ = 54°
In ΔXYZ, we have, ∠LZJ + ∠KYJ + ∠KXL = 180° based on the sum of the interior angles of a triangle postulate
∴ ∠LZJ = 180° - (∠KYJ + ∠KXL) = 180° - (54° + 62°) = 64°
∠LZJ = 64°
The segment
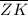 bisects ∠LZJ to form ∠PZL and ∠PZJ
bisects ∠LZJ to form ∠PZL and ∠PZJ
Therefore, ∠PZL = ∠PZJ
∠LZJ = ∠PZL + ∠PZJ = 2 × ∠PZL = 64°
∠PZL = 64°/2 = 32° = ∠PZJ
In ΔZPX, we have;
∠PZL + ∠LXP + ∠ZPX = 180° based on the sum of the interior angles of a triangle postulate
∠ZPX = 180° - (∠PZL + ∠LXP) = 180° - (32° + 31°) = 63°
∠ZPX = 63°
The measure of ∠ZPX = 63°