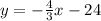Question

Please help 30 points!!'

Write an equation based on the following conditions in slope/y intercept form
Perpendicular to 3x-4y=9 through (-15,-4)
also can yall provide some shown work as my geometry teacher asked for shown work

Answer 1

The equation of line perpendicular to given line passing through (-15,-4) is:

`y = -(4)/(3)x-24`

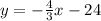
Explanation:

Given equation is:

`3x-4y = 9`

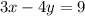
The given equation is in standard form. We have to convert it into slope intercept form first.

The slope intercept form is:

`y = mx+b`

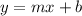
So,

`3x-4y=9\\3x-9 = 4y\\4y = 3x-9\\(4y)/(4) = (3x-9)/(4)\\y = (3)/(4)x - (9)/(4)`

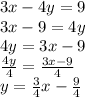
The co-efficient of x is the slope of the line.

m = 3/4

The product of slopes of two perpendicular lines is: -1

Let m1 be the slope of line perpendicular to given line then

`m.m_1 =-1\\(3)/(4) . m_1 = -1\\m_1 = -1 * (4)/(3) \\m_1 = -(4)/(3)`

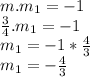
Putting in slope-intercept form

`y = m_1x+b\\y = -(4)/(3)x+b`

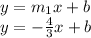
To find the value of b, putting (-15,-4) in equation

`-4 = -(4)/(3)(-15) +b\\-4 = 20+b\\-4-20 = b\\b = -24`

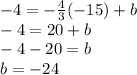
The equation will be:

`y = -(4)/(3)x-24`

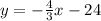
Hence,

The equation of line perpendicular to given line passing through (-15,-4) is:

`y = -(4)/(3)x-24`