Question

Someone, please help!! if u actually know how to do it

Answer 1

`distance=\sqrt{(-2-(-5))^(2) +(6-(-10))^(2)}`

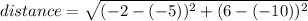
distance = 16.2788

Explanation:

This question is asking you to correctly apply the distance formula. This formula determines the straight line distance between two points by applying Pythagorean's Theorem (
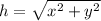`h = \sqrt{x^(2)+y^(2) }`). The distance formula can be thought of as
`distance=\sqrt{(x_(1)-x_(2))^(2) +(y_(1)-y_(2))^(2)}`. It doesn't matter which order you put your coordinates into the equation as long as it's the square root of the change in x-coordinates squared + change in y-coordinates squared.

Step 1: change in x-coordinates

x1 = -2

x2 = -5

x1 - x2 = -2 - (-5) = 3

Step 2: change in y-coordinates

y1 = 6

y2 = -10

y1 - y2 = 6 - (-10) = 16

Step 3: plug into distance formula

`distance=\sqrt{(-2-(-5))^(2) +(6-(-10))^(2)}`

`distance=\sqrt{(3)^(2) +(16)^(2)}`

`distance=√(9 +256)`

`distance=√(265)`

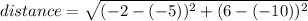
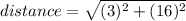
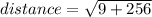
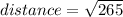
distance = 16.2788