Question

I need it within tomorrow please

Consider the following sequence of successive numbers of the 2k
-th power:
1, 2
2
k
, 3
2
k
, 4
2
k
, 5
2
k
, ...
Show that the difference between the numbers in this sequence is odd for all k ∈ N.

Answer 1

Any even number raised to any power will remain even. (e.g. 2² = 4, 2³ = 8, etc)

Any odd number raised to any power will remain odd. (e.g. 1² = 1³ = ... = 1, 3⁴ = 81, etc)

So
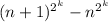`(n+1)^(2^k)-n^(2^k)` will always be even, since both

[even] - [odd] = [odd]

and

[odd] - [even] = [odd]