Question

Which equation has the steepest parabola?

A. (x+2)2=−0.5(y+3)
B. (x−1)2=5(y+3)
C. x2=8(y−1)
D. (x+2)2=−10y

Answer 1

Given:

The equations of parabolas in the options.

To find:

The steepest parabola.

Solution:

We know that, if a parabola is defined as

`(y-k)=n(x-h)^2`

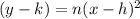
Then, the greater absolute value of n, the steeper the parabola.

It can be written as

`(1)/(n)(y-k)=(x-h)^2`

`p(y-k)=(x-h)^2`

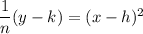
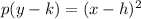
where
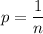`p=(1)/(n)`, the smaller absolute value of p, the steeper the parabola.

Now, find the value of |p| for eac equation

For option A,
`|-0.5|=0.5`

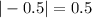
For option B,
`|5|=5`

For option C,
`|8|=8`

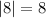
For option D,
`|-10|=10`

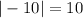
Since, the equation is option A has smallest value of |p|, therefore, the equation
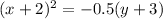`(x+2)^2=-0.5(y+3)` represents the steepest parabola.

Hence, the correct option is A.