Question

Slope = 3/4 , goes through the point (0, 6)

Answer 1

y = 3/4x + 6

Explanation:

Answer 2

The equation of the line in point-slope form, passing through (0, 6) with a slope of 3/4, is
`\(y - 6 = (3)/(4)x\)`. Simplifying, it becomes
`\(y = (3)/(4)x + 6\)`.

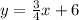The point-slope form of the equation of a line is given by:

`\[ y - y_1 = m(x - x_1) \]`

where
`\((x_1, y_1)\)` is a point on the line, and m is the slope.

In this case, the point is (0, 6), and the slope is 3/4. Plugging these values into the point-slope form:

`\[ y - 6 = (3)/(4)(x - 0) \]`

Simplifying:

`\[ y - 6 = (3)/(4)x \]`

This is the equation of the line in point-slope form. If you want to express it in slope-intercept form y = mx + b, you can further simplify:

`\[ y = (3)/(4)x + 6 \]`

The complete question is:

What is the equation of the line (in point-slope form) that passes through the point (0, 6) and has a slope of 3/4?