Question

Four students are trying to determine what number must replace the question (x^2)^7=x^4*x^8 in order to make it true

Joe said the answer is 6. Sam said it is impossible to answer.
Peter said the answer is 32. Alex said the answer is 16.
Who is correct? Explain why.

Answer 1

Let's solve ourselves instead of believing anyone

`\\ \rm\Rrightarrow (x^2)^7=x^4x^8`

• a^m+a^n=a^m+n

`\\ \rm\Rrightarrow x^(14)=x^(4+8)`

`\\ \rm\Rrightarrow x^(14)=x^(12)`

`\\ \rm\Rrightarrow x^(14)-x^(12)=0`

`\\ \rm\Rrightarrow x^(12)(x^2-1)=0`

`\\ \rm\Rrightarrow x^2-1=0`

`\\ \rm\Rrightarrow x^2=1`

`\\ \rm\Rrightarrow x=\pm 1`

• 0 is also a solution

Answer 2

Joe is correct

Explanation:

Given equation:

`(x^2)^?=x^4 \cdot x^8`

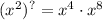
The exponent outside the bracket is a question mark and the students are trying to determine the value of the question mark.

For ease of answering, let y be the unknown number (question mark):

`\implies (x^2)^y=x^4 \cdot x^8`

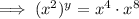
First, simplify the equation by applying exponent rules to either side of the equation:

`\textsf{Apply exponent rule} \quad (a^b)^c=a^(bc)\quad\textsf{to the left side}:`

`\implies (x^2)^y=x^4 \cdot x^8`

`\implies x^(2y)=x^4 \cdot x^8`

`\textsf{Apply exponent rule} \quad a^b \cdot a^c=a^(b+c) \quad \textsf{to the right side}:`

`\implies x^(2y)=x^4 \cdot x^8`

`\implies x^(2y)=x^(4+8)`

`\implies x^(2y)=x^(12)`

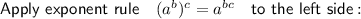
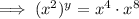
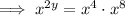
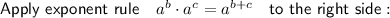
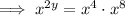
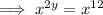
Now, apply the exponent rule:

`x^(f(x))=x^(g(x)) \implies f(x)=g(x)`

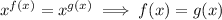
Therefore,

`x^(2y)=x^(12)\implies 2y=12`

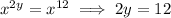
Finally, solve for y:

`\implies 2y=12`

`\implies 2y / 2 = 12 / 2`

`\implies y=6`

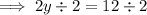
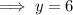
Therefore, Joe is correct as the unknown number is 6.