Question

Una curva de radio R = 75 [m] tiene un peralte hecho de tal forma que un auto andando a v1 = 35 [m/s] no derrape incluso con el piso congelado (sin roce). ¿Cuál es el coeficiente de roce estático mínimo necesario entre las ruedas y el pavimento para que, en un día seco y soleado, el auto no derrape cuando avanza a v2 = 118 [m/s]?

Answer 1

053.

Step-by-step explanation:

Given that the radius of curvature of the path, R = 75 m.

Speed of the car on that path ,
`v_1 = 35 m/s`

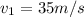
The centripetal force,
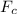`F_c` acting on the body having mass, m, when it moves with the velocity v on curved path having radiusR

Ris
`F_c = mv^2/R`

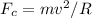
Gravitational force,
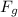`F_g` = mg.

Let tha angle of superelevation is
`\theta.`

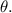
As the car does not skid even with zero friction, so

`mg\sin\theta = (mv_1^2)/2 \cos\theta`

`\Rightarrow \tan\theta = v_1^2/2g=\cdots(i)`

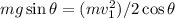
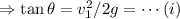
On sunny day, let the minimun static friction coefficient between the wheels and the pavement is
`\mu.`

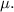
As
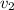`v_2` = 118 m/s is greater than v_so the car tends to skid in upper direction and the frictional

force,f, will acts is downward direction.

As there is no skidding, so

`f+ mg\sin\theta= (m(v_2)^2)/R\cos\theta`

`\Rightarrow f=(m(v_2)^2)/R\cos\theta - mg\sin\theta`

where
`f= \mu N.`

`So, \mu = \frac {(m(v_2)^2)/R\cos\theta - mg\sin\theta}{N} \cdots(ii)`

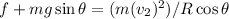
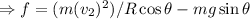
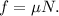
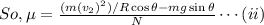
Where N is the normal reaction can be determined by balancing the force in perpendicular direction of the plane.

`N= mg\cos\theta+\frac {m(v_2)^2}{R}\sin\theta`

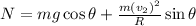
From equation (ii)

`\mu = \frac {(m(v_2)^2)/R\cos\theta - mg\sin\theta}{mg\cos\theta+\frac {m(v_2)^2}{R}\sin\theta}`

`=(-g\tan\theta+v^2/R)/(v_2^2\tan\theta+g)`

`= \frac {(m(v_2)^2)/R\cos\theta - mg\sin\theta}{mg\cos\theta+\frac {m(v_2)^2}{R}\sin\theta}`

`=(-g(v_1^2/2g)+v^2/R)/(v_2^2(v_1^2/2g)+g)`

`= (v_2^2/R-v_1^2/R)/(g+v_2^2/R* v_1^2/Rg)`

`=(118^2/75-35^2/75)/(9.81+118^2/75* 35^2/(75* 9.81))`

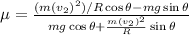
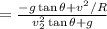
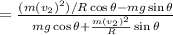
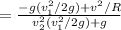
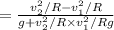
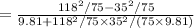
=0.53

Hence, the minimum coefficient of friction is 0.53.