Question

2(x + 0.7) = 6(x – 0.8)​ well what i got for this is 2x + 1.4 = 6x - 4.8 -2 -2 1.4 = 4x - 4.8 +4.8 +4.8 so i do i finish this equation i need the answer how do i finish this Equation?

Answer 1

1.55

Explanation:

`2(x + 0.7) = 6(x – 0.8)​`

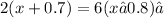
Using the distributive property of addition over multiplication we get

`2x+1.4=6x-4.8`

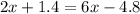
Take the like terms to one side and change their signs accordingly

`1.4+4.8=6x-2x`

`\Rightarrow 6.2=4x`

`\Rightarrow x=(6.2)/(4)`

`\Rightarrow x=1.55`

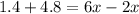
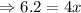
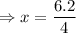
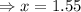
The value of
`x` is 1.55.

In order to make sure this value is correct we can substitute the value of x in the equation

`2(1.55+0.7)=6(1.55-0.8)\\\Rightarrow 2* 2.25=6* 0.75\\\Rightarrow 4.5=4.5`

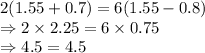
So, both sides are equal hence the value of
`x`is 1.55.