Question

A car’s brakes decelerate it at a rate of -2.40 m/s2. If the car is originally travelling at 13 m/s and comes to a stop, then how far, in meters, will the car travel during that time?

Answer 1

Approximately
`35.2\; \rm m`.

Step-by-step explanation:

Given:

Initial velocity:
`u = 13\; \rm m \cdot s^(-1)`.

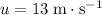Acceleration:
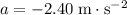`a = -2.40\; \rm m \cdot s^(-2)` (negative because the car is slowing down.)

Implied:

Final velocity:
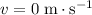`v = 0\; \rm m \cdot s^(-1)` (because the car would come to a stop.)

Required:

Displacement,
`x`.

Not required:

Time taken,
`t`.

Because the time taken for this car to come to a full stop is not required, apply the SUVAT equation that does not involve time:

`\begin{aligned} x &= (v^2 - u^2)/(2\, a) \\ &= \frac{{\left(0\; \rm m \cdot s^(-1)\right)}^2 - {\left(13\; \rm m \cdot s^(-1)\right)}^2}{2* \left(-2.40\; \rm m\cdot s^(-2)\right)} \approx 35.2\; \rm m \end{aligned}`.

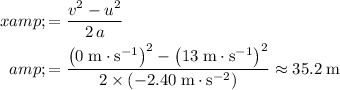In other words, this car would travel approximately
`35.2\; \rm m` before coming to a stop.