Question

The radius of the base of a cylinder is increasing at a rate of 11 meter per hour and the height of the cylinder is decreasing at a rate of 44 meters per hour. At a certain instant, the base radius is 55 meters and the height is 88 meters. What is the rate of change of the volume of the cylinder at that instant (in cubic meters per hour)?

Answer 1

The volume of the cylinder is decreasing at a rate of 83629.2 m³/h.

Explanation:

The volume of a is given by:

`V = \pi r^(2)h`

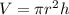
Where:

r: is the radius = 55 m

h: is the height = 88 m

We can express the rate of change of the volume of the cylinder as follows:

`(dV)/(dt) = \pi[h(2rdr)/(dt) + r^(2)(dh)/(dt)]`

If dr/dt = 11 m/h and dh/dt = -44m/h, we have:

`(dV)/(dt) = \pi[88 m*2*55 m*11 m/h + (55 m)^(2)*(-44 m/h)] = -83629.2 m^(3)/h`

Therefore, the volume of the cylinder is decreasing at a rate of 83629.2 m³/h.

I hope it helps you!