Question

What is the equation of a line that passes through (-7, 3) and is perpendicular to -5/3x = 1/4y -8

Select all answers that apply
Y = 3/20x + 81/20
Y-3 = 3/20(x+7)
Y-3 = -20/3(x+7)
Y = -20/3x -32
3x -20y = -81
The answer can be anything thing that occurs during solving the problem or is the answer.

Answer 1

The 1st, 2nd and 5th options are correct.

Explanation:

The equation of a line can be written in the form of y=mx+c, where m is the gradient and c is the y-intercept.

①Rewrite the given equation into the form of y=mx+c to find the gradient.

`- (5)/(3) x = (1)/(4) y - 8 \\ (1)/(4) y = - (5)/(3) x + 8 \\ y = - (20)/(3) x + 32`

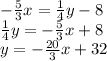
Thus, the gradient of the given equation is
`- (20)/(3)`.

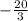② Find gradient of unknown line.

The product of the gradients of perpendicular lines is -1.

Let m be the gradient of the unknown line.

`- (20)/(3) m = - 1 \\ m = - 1 / ( - (20)/(3) ) \\ m = - 1 * ( - (3)/(20) ) \\ m = (3)/(20)`

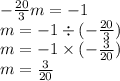
③Substitute the value of m into the equation.

`y = (3)/(20) x + c`

④ Find the value of c by substituting a pair of coordinates.

When x= -7, y= 3,

`3 = (3)/(20) ( - 7) + c \\ 3 = - (21)/(20) + c \\ c = 3 + (21)/(20) \\ c = 4 (1)/(20)`

Thus, the equation of the line is
`y = (3)/(20) x + 4 (1)/(20)`.

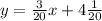Thus, the 4th option is incorrect.

Writing c as an improper fraction,

`y = (3)/(20)x + (81)/(20)`

Thus, the 1st option is correct.

-3 from both sides of the equation:

`y - 3 = (3)/(20) x + (21)/(20)`

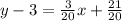
Factorise 3/20 out of the right hand side:

`y - 3 = (3)/(20) (x + 7)`

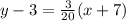
Thus, the 2nd option is correct.

The 3rd option is incorrect as factorising -20/3 out would leave us with -0.0225 as the coefficient of x.

Let's look at the 5th option.

`y = (3)/(20) x + 4 (1)/(20)`

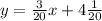
×20 on both sides:

`20y = 3x + 81`

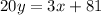
-20y on both sides:

`3x - 20y + 81 = 0`

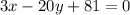
-81 on both sides:

`3x - 20y = - 81`

Thus, the 5th option is also correct.