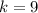Question

Given that k-5, k+7, k+55 are three consecutive terms in a geometric sequence, solve for k​

Answer 1

`k = 9`

Explanation:

Given:

Consecutive Terms: k-5, k+7, k+55

Required:

Determine the value of k

To do this, we make use of the concept of common ratio.

The common ratio (r) of a geometric sequence is:

`r = (T_(n))/(T_(n-1))`

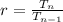
In other words:

`r = (T_3)/(T_2) = (T_2)/(T_1)`

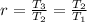
Where 1, 2 and 3 represents the terms of the progression/sequence

So:

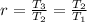`r = (T_3)/(T_2) = (T_2)/(T_1)` becomes

`(k+55)/(k+7) = (k+7)/(k-5)`

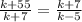
Cross Multiply:

`(k+55)(k-5) = (k+7)(k+7)`

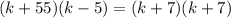
Open Brackets

`k^2 + 55k - 5k - 275 = k^2 + 7k + 7k + 49`

`k^2 + 50k- 275 = k^2 + 14k + 49`

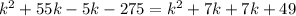
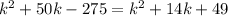
Collect Like Terms

`k^2 - k^2 + 50k-14k = 275 + 49`

`36k = 324`

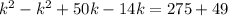
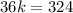
Solve for k

`k = 324/36`

`k = 9`